milivp.blogg.se - Projectile motion calculator vertical

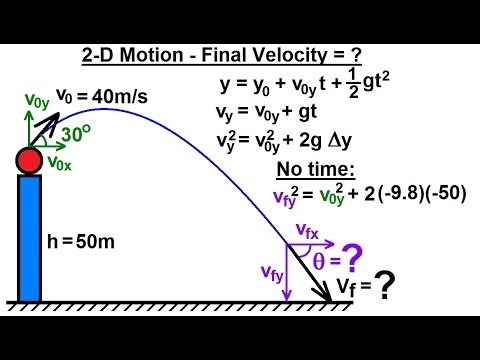
This result is consistent with the fact that the ball is impacting at a point on the other side of the apex of the trajectory and therefore has a negative y component of the velocity. (b) The negative angle means the velocity is 36.9 ° 36.9 ° below the horizontal at the point of impact. Thus, any projectile that has an initial vertical velocity of 21.2 m/s and lands 10.0 m above its starting altitude spends 3.79 s in the air. Significance(a) As mentioned earlier, the time for projectile motion is determined completely by the vertical motion. Solve for the magnitude and direction of the displacement and velocity using Recombine quantities in the horizontal and vertical directions to find the total displacement s → s → and velocity v →.The problem-solving procedures here are the same as those for one-dimensional kinematics and are illustrated in the following solved examples. Note that the only common variable between the motions is time t. Solve for the unknowns in the two separate motions: one horizontal and one vertical.Use the kinematic equations for horizontal and vertical motion presented earlier. Treat the motion as two independent one-dimensional motions: one horizontal and the other vertical.The magnitudes of the components of velocity v → v → are v x = v cos θ and v y = v sin θ, v x = v cos θ and v y = v sin θ, where v is the magnitude of the velocity and θ is its direction relative to the horizontal, as shown in Figure 4.12.

The magnitudes of the components of displacement s → s → along these axes are x and y.

Resolve the motion into horizontal and vertical components along the x- and y-axes.

The magnitudes of these vectors are s, x, and y. Figure 4.11 illustrates the notation for displacement, where we define s → s → to be the total displacement, and x → x → and y → y → are its component vectors along the horizontal and vertical axes, respectively. In other cases we may choose a different set of axes. It is not required that we use this choice of axes it is simply convenient in the case of gravitational acceleration. (This choice of axes is the most sensible because acceleration resulting from gravity is vertical thus, there is no acceleration along the horizontal axis when air resistance is negligible.) As is customary, we call the horizontal axis the x-axis and the vertical axis the y-axis. The key to analyzing two-dimensional projectile motion is to break it into two motions: one along the horizontal axis and the other along the vertical. We discussed this fact in Displacement and Velocity Vectors, where we saw that vertical and horizontal motions are independent. The most important fact to remember here is that motions along perpendicular axes are independent and thus can be analyzed separately. In this section, we consider two-dimensional projectile motion, and our treatment neglects the effects of air resistance. The motion of falling objects as discussed in Motion Along a Straight Line is a simple one-dimensional type of projectile motion in which there is no horizontal movement. Such objects are called projectiles and their path is called a trajectory.

Some examples include meteors as they enter Earth’s atmosphere, fireworks, and the motion of any ball in sports. The applications of projectile motion in physics and engineering are numerous. Projectile motion is the motion of an object thrown or projected into the air, subject only to acceleration as a result of gravity. Calculate the trajectory of a projectile.Find the time of flight and impact velocity of a projectile that lands at a different height from that of launch.Calculate the range, time of flight, and maximum height of a projectile that is launched and impacts a flat, horizontal surface.Use one-dimensional motion in perpendicular directions to analyze projectile motion.By the end of this section, you will be able to: